|
|
BERNOULLI EFFECT (BERNOULLI PRESSURE DIFFERENCE)
|
Description |
|
If in a steady-state situation, along a horizontal flow line in a non-viscous fluid, the flow speed is not the same at two different points, the fluid pressure will be different at these points. We can say that speed changes require (or establish) pressure differences.
|
|
|

|
Relations |
|
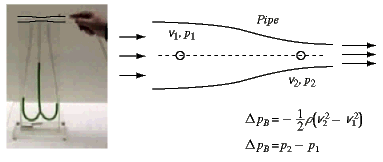
Left: Venturi pipe with pressure sensors; air is blown into the pipe on the right side.
Right: Narrowing of pipe leads to increase of flow speed and to a reduction of the fluid pressure (see Continuity Equation):
delta_pB = – 0.5*rho*(v2^2 – v1^2)
delta_pB: pressure difference because of speed change; v: flow speed; rho: density of fluid; p: fluid pressure.
If there is no friction (or no other process between Points 1 and 2), the pressure difference delta_pB equals the actual pressure difference p2–p1.
|
|
|

|
Remarks |
|
Bernoulli's theorem can be found by integrating the momentum equation along a flow line. Alternatively, it can be derived based on an input-output analysis using the balance of energy of the participating systems.
It holds for gases (air) if the density does not vary too greatly.
|
|
|

|
Symbols |
|
p, delta_p, rho, v |
Units |
|
[p] = Pa, [rho] = kg/m^3, [v] = m/s |
Synonyms |
|
|
Related to |
|
Bernoulli theorem |
Translations |
|
(German) Bernoulli-Effekt
|
|
|

|


