There are two important special cases of flows, namely laminar and turbulent flows, respectively. The flow typically is laminar if the Reynolds number is below a critical value.

The flow can be expressed in terms of the appropriate flow characteristic which is linear for laminar flow. For laminar flow in circular pipes, we can use the law of Hagen and Poiseuille.

I_V = G_V · ∆p_R

I_V = 1/R_V · ∆p_R

The factor preceding ∆p_R is the hydraulic conductance G_V. (Alternatively, we can write the relation using the inverse of the conductance, the hydraulic resistance R_V.) For laminar flow in tubes with a circular cross secion, we have the simple form of the law of Hagen and Poiseuille (also called the law of Poiseuille):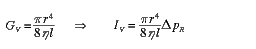

eta: viscosity; r: radius of pipe; l: length of pipe; IV: volume flux, ∆p_R: resistive pressure difference.

The flow law in pipes is often written in the general form

(see turbulent flow laws). With

  f = 64/Re,

where Re is the Reynolds number, we obtain the law of Hagen and Poiseuille.

laminar flow, flow characteristic, Hagen and Poiseuille, conductive transport, turbulent flow laws, turbulent flow,

Flows in pipes are laminar if Re < 2300 (newer research sets the critical value for Re at lower values of around 800-1000, depending on circumstances).

laminare Strömungsgesetze