| |
 |
A straight walled tank is filled with rape seed oil. At the bottom, a horizontal glass pipe with constant diameter is fitted to the tank.
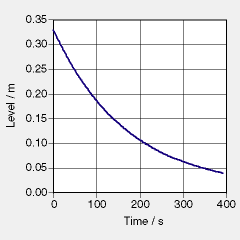
The oil level is shown as a function of time in the graph on the right. The diameter of the tank is 20.0 cm. The length of the pipe is 1.055 m, its radius is 8.1 mm. The density of rape seed oil is 910 kg/m^3. Data found in  Single_Tank_Oil.
-
Determine as carefully as possible the rate of change of the level right at the beginning (t = 0). How long would it take for the tank to drain completely if the outflow stayed constant at its initial rate?
-
How long does it take for the level of oil to have decreased to 37% of its initial value (= 1/e of the initial value)? Compare to the previous result for how long it takes to drain the tank at the (constant) initial rate. [The result is called the (capacitive) time constant of this system.]
-
Calculate the current of oil and the flow speed at t = 0.
-
Determine the initial pressure difference along the pipe. Then calculate the hydraulic conductance (and the resistance).
-
Multiply the values of the resistance and the capacitance. Compare to the value of the time constant obtained above.
|
|
-
From the data gained so far, determine the viscosity of rape seed oil. Compare this to values found in the literature.
-
Determine the current at several points in time. Sketch the flow as a function of time and as a function of fluid level. Do this graphically first, and then again using a spreadsheet and the data file.
Click HERE to obtain pdf
|
